Segitiga Daya

Daya Aktif, Daya Reaktive dan Daya Semu

Telah dipahami dan dianalisa tentang teori daya listrik pada arus bolak-balik, bahwa disipasi daya pada beban reaktif (induktor dan kapasitor) relatif kecil, namun fakta menunjukkan bahwa pada beban reaktif terjadi sentakan arus dan tegangan jatuh pada terminalnya, ini memberi kesan seolah-olah beban reaktif benar-benar mendisipasi daya secara nyata. Fakta ini disebut sebagai Daya Reaktif (Reactive Power) yang dimensi ukurnya dalam satuan VAR (Volt-Amps-Reaktif) bukan dalam satuan Watt.

Simbol matematika untuk daya reaktif disepakati adalah Q dan besar daya sebenarnya yang digunakan atau yang hilang (disipasi daya) dalam rangkaian disebut Daya Aktif (True Power) yang dimensi ukurnya dalam satuan Watt dan disepakati dilambangkan dengan huruf besar P. Kombinasi dari daya reaktif dan daya aktif disebut Daya Semu (Apparent Power) yang merupakan produk dari suatu rangkaian yang memiliki tegangan dan arus tanpa merujuk pada sudut phasa. Dimensi ukur dari daya semu dalam satuan VA (Volt-Amps) dan kesepakatan lambang dengan huruf S.

Sebagai sebuah kaidah, daya aktif merupakan fungsi dari elemen rangkaian disipasi yang umumnya berupa resistansi (R) dan daya reaktif merupakan fungsi dari suatu elemen rangkaian reaktansi (X) dan umumnya dapat berupa induktansi (L) atau capasitansi (C). Daya semu adalah fungsi dari suatu rangkaian impedansi total (Z).
Karena kita berurusan dengan perhitungan besaran skalar dari daya yang kompleks mulai dari besaran seperti tegangan, arus dan impedansi maka harus diwakili oleh magnitudo polar, bukan dengan bilangan riil atau imajiner dari komponen rectangular.

Sebagai contoh, jika saya menghitung daya aktif dari arus dan resistansi, saya harus menggunakan magnitudo polar untuk arus dan bukan hanya bilangan riil atau imajiner saja bagian dari arus dan jika saya menghitung daya semu dari tegangan dan impedansi, kedua besaran komplek tersebut sebelumnya harus diturunkan atau direduksi ke magnitudo polar mereka untuk aritmatika skalar.
Ada beberapa persamaan yang menghubungkan ketiga jenis daya yaitu resistansi, reaktansi dan impedansi yang semuanya menggunakan besaran skalar:

Perlu diketahui bahwa ada dua persamaan untuk perhitungan daya aktif dan daya reaktif dan ada tiga persamaan untuk perhitungan daya semu. Periksa rangkaian berikut dan lihat bagaimana ketiga jenis daya saling berhubungan: sebuah beban resistif murni pada Gbr.1, beban reaktif murni pada Gbr.2 dan beban campuran resistif dan reaktif pada Gbr.3 di bawah ini.

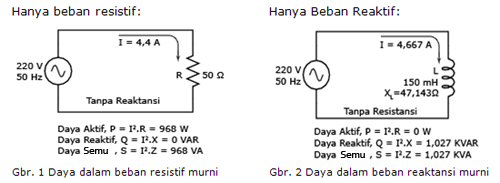
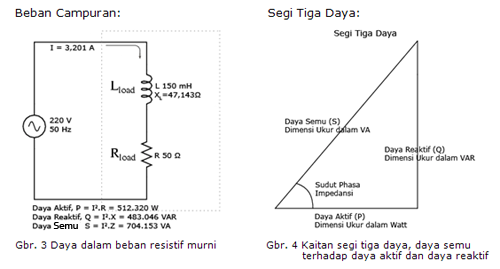
Ketiga jenis daya aktif, reaktif, dan semu berhubungan satu sama lain dalam bentuk trigonometri. Hubungan antara daya tersebut dinamakan Segi Tiga Daya (The Power Triangle) seperti diperlihatkan pada Gbr.4 di atas.

Gunakan hukum rumus trigonometri untuk menghitung panjang dari setiap sisi atau jumlah besaran seluruh daya, jika telah diketahui panjang dua sisi lainnya atau panjang salah satu sisi dengan sudutnya.

Kesimpulan:

Energi yang disipasi atau dihamburkan oleh beban disebut sebagai daya aktif. Daya aktif dilambangkan oleh huruf P dan diukur dalam satuan W (Watt).

Energi hanya terserap dan kembali ke sumbernya karena sifat beban yang reaktif ini maka disebut sebagai daya reaktif. Daya reaktif dilambangkan dengan huruf Q dan diukur dalam satuan VAR (Volt-Amps-reaktif).
Energi total dalam rangkaian arus bolak-balik, baik dihamburkan, diserap ataupun yang kembali disebut sebagai daya semu. Daya semu dilambangkan dengan huruf S dan diukur dalam satuan VA (Volt-Amps).

Ketiga jenis daya secara trigonometri terkait satu sama lain. Dalam segi tiga siku-siku, P adalah garis mendatar yang mengapit sudut, Q adalah garis tegak dihadapan sudut dan S adalah garis sisi miring dan mengapit sudut. Sudut yang diapit garis adalah sudut phasa rangkaian impedansi (Z).